È bello compiere gli anni. In particolar modo per i compleanni con un numero primo.
Per altri pipponi matematici, cito da Wikipedia:
- È il dodicesimo numero primo, dopo il 31 e prima del 41.
- È un numero primo irregolare.
- Non ci sono altri numeri primi q tali che la lunghezza di periodo del relativo reciproco, 1/37, è equivalente alla lunghezza di periodo del reciproco di q, 1/q.
- È un numero primo cubano della forma
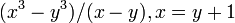 .
. - È un primo permutabile con 73.
- È un numero esagonale centrato e un numero stellato.
- Non è la somma di due numeri primi.
- Se un multiplo di tre cifre di 37 viene ciclicamente permutato, per esempio 481 diventa 148 o 814,, allora i numeri risultanti sono ancora multipli di 37. L’unico altro numero che ha questa proprietà nell’ambito delle tre cifre è 27.
- È l’unico numero di due cifre che moltiplicato per la somma delle sue cifre dia un prodotto uguale alla somma dei cubi di tali cifre:

- Ogni numero naturale è la somma di al più 37 quinte potenze.
- È la somma di due quadrati, 37 = 12 + 62.
- 1/37 = 0,027027027…., e 1/27 = 0,037037037…